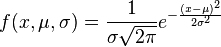Does WAR undervalue injured superstars?
In an article last month, "Ain't Gonna Study WAR No More" (subscription required), Bill James points out a flaw in WAR (Wins Above Replacement), when used as a one-dimensional measure of player value.
Bill gives an example of two hypothetical players with equal WAR, but not equal value to their teams. One team has Player A, an everyday starter who created 2.0 WAR over 162 games. Another team has Player B, a star who normally produces at the rate of 4.0 WAR, but one ear created only 2.0 WAR because he was injured for half the season.
Which player's team will do better? It's B's team. He creates 2.0 WAR, but leaves half the season for someone from the bench to add more. And, since bench players create wins at a rate higher than 0.0 -- by definition, since 0.0 is the level of player that can be had from AAA for free -- you'd rather have the half-time player than the full-time player.
This seems right to me, that playing time matters when comparing players of equal WAR. I think we can tweak WAR to come up with something better. And, even if we don't, I think the inaccuracy that Bill identified is small enough that we can ignore it in most cases.
------
First: you have to keep in mind what "replacement" actually means in the context of WAR. It's the level of a player just barely not good enough to make a Major League Roster. It is NOT the level of performance you can get off the bench.
Yes, when your superstar is injured, you often do find his replacement on the bench. That causes confusion, because that kind of replacement isn't what we really mean when we talk about WAR.
You might think -- *shouldn't* it be what we mean? After all, part of the reason teams keep reasonable bench players is specifically in case one of the regulars gets injured. There is probably no team in baseball, when their 4.0 WAR player goes down the first day of the season, can't replace at least a portion of those wins from an available player. So if your centerfielder normally creates 4.0 WAR, but you have a guy on the bench who can create 1.0 WAR, isn't the regular really only worth 3.0 wins in a real-life sense?
Perhaps. But then you wind up with some weird paradoxes.
You lease a blue Honda Accord for a year. It has a "VAP" (Value Above taking Public Transit) of, say $10,000. But, just in case the Accord won't start one morning, you have a ten-year-old Sentra in the garage, which you like about half as much.
Does that mean the Accord is only worth $5,000? If it disappeared, you'd lose its $10,000 contribution, but you'd gain back $5,000 of that from the Sentra. If you *do* think it's only worth $5,000 ... what happens if your neighbor has an identical Accord, but no Sentra? Do you really want to decide that his car is twice as valuable as yours?
It's true that your Accord is worth $5,000 more than what you would replace it with, and your neighbor's is worth $10,000 more than what would he would replace it with. But that doesn't seem reasonable as a general way to value the cars. Do you really want to say that Willie McCovey has almost no value just because Hank Aaron is available on the bench?
------
There's also another accounting problem, one that commenter "Guy123" pointed out on Bill's site. I'll use cars again to illustrate it.
Your Accord breaks down halfway through the year, for a VAP of $5,000. Your mother has only an old Sentra, which she drives all year, for an identical VAP of $5,000.
Bill James' thought experiment says, your Accord, at $5,000, is actually worth more than your mother's Sentra, at $5,000 -- because your Accord leaves room for your own Sentra to add value later. In fact, you get $7,500 in VAP -- $5,000 from half a year of the Accord, and $5,000 from half a year of the Sentra.
Except that ... how do you credit the Accord for the value added by the Sentra? You earned a total of $7,500 in VAP for the year. Normal accounting says $5,000 for the Accord, and $2,500 for the Sentra. But if you want to give the Accord "extra credit," you have to take that credit away from the Sentra! Because, the two still have to add up to $7,500.
So what do you do?
------
I think what you do, first, is not base the calculation on the specific alternatives for a particular team. You want to base the calculation on the *average* alternative, for a generic team. That way, your Accord winds up worth the same as your neighbor's.
You can call that, "Wins Above Average Bench." If only 1 in 10 households has a backup Sentra, then the average alternative is one tenth of $5,000, or $500. So the Accord has a WAAB of $9,500.
All this needs to happen because of a specific property of the bench -- it has better-than-replacement resources sitting idle.
When Jesse Barfield has the flu, you can substitute Hosken Powell for "free" -- he would just be sitting on the bench anyway. (It's not like using the same starting pitcher two days in a row, which has a heavy cost in injury risk.)
That wouldn't be the case if teams didn't keep extra players on the bench, like if the roster size for batters were fixed at nine. Suppose that when Jesse Barfield has the flu, you have to call Hosken Powell up from AAA. In that case, you DO want Wins Above Replacement. It's the same Hosken Powell, but, now, Powell *is* replacement, because replacement is AAA by definition.
Still, you won't go too wrong if you just stick to WAR. In terms of just the raw numbers, "Wins Above Replacement" is very close to "Wins Above Average Bench," because the bottom of the roster, the players that don't get used much, is close to 0.0 WAR anyway.
For player-seasons between 1982 and 1991, inclusive, I calculated the average offensive expectation (based on a weighted average of surrounding seasons) for regulars vs. bench players. Here are the results, in Runs Created per 405 outs (roughly a full-time player-season), broken down by "benchiness" as measured by actual AB that year:
500+ AB: 75
401-500: 69
301-400: 65
201-300: 62
151-200: 60
101-150: 59
76-100: 45
51- 75: 33
A non-superstar everyday player, by this chart, would probably come in at around 70 runs. A rule of thumb is that everyday players are worth about 2.0 WAR. So, 0.0 WAR -- replacement level -- would about 50 runs.
The marginal bench AB, the ones that replace the injured guy, would probably come from the bottom four rows of the chart -- maybe around 55. That's 5 runs above replacement, or 0.5 wins.
So, the bench guys are 0.5 WAR. That means when the 4.0 guy plays half a season, and gets replaced by the 0.5 guy for the other half, the combination is worth 2.25 WAR, rather than 2.0 WAR. As Bill pointed out, the WAR accounting credits the injured star with only 2.0, and he still comes out looking only equally as good as the full-time guy.
But if we switch to WAAB ... now, the full-time guy is 1.5 WAAB (2.0 minus 0.5). The half-time star is 1.75 WAAB (4.0 minus 0.5, all divided by 2). That's what we expected: the star shows more value.
But: not by much. 0.25 wins is 2.5 runs, which is a small discrepancy compared to the randomness of performance in general. And even that discrepancy is random, since something as large as a quarter of a win only shows up when a superstar loses half the season to injury. The only time when it's large and not random is probably star platoon players -- but there aren't too many of those.
(The biggest benefit to accounting for the bench might be when evaluating pitchers, who, unlike hitters, vary quite a bit in how much they're physically capable of playing.)
I don't see it as that a big deal at all. I'd say, if you want, when you're comparing two batters, give the less-used player a bonus of 0.1 WAR for each 100 AB of playing time.
Of course, that estimate is very rough ... the 0.1 wins could easily be 0.05, or 0.2, or something. Still, it's still going to be fairly small -- small enough that I'd be it wouldn't change too many conclusions that you'd reach if you just stuck to WAR.
Labels: Bill James, WAR